Homework 2

Derive equations by hand on paper (or on a tablet). Solve for transfer functions using Matlab. Upload pictures of your work to Blackboard for credit.

Problem 1

Find the state-space representation of the circuit shown below. Assume the output is $v_{o}(t)$.

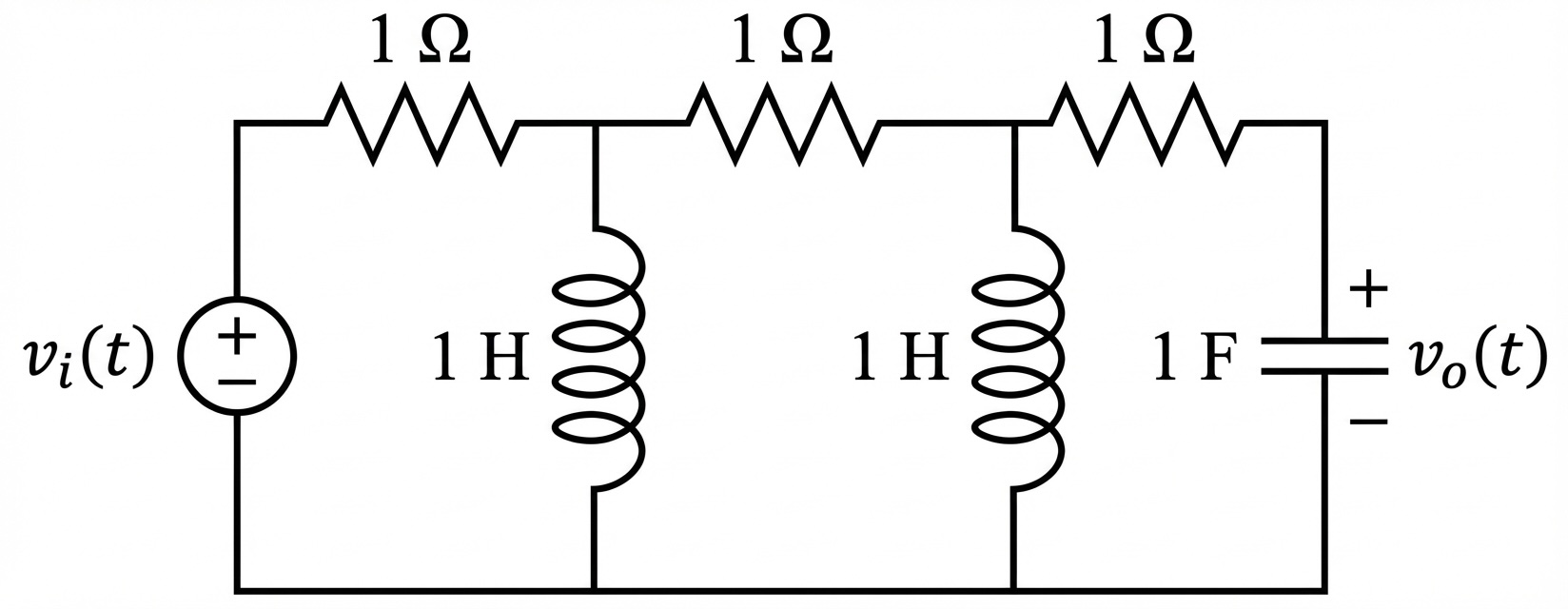
Problem 2

Find the state-space representation of the system shown below. Assume $x_{3}(t)$ is the output.

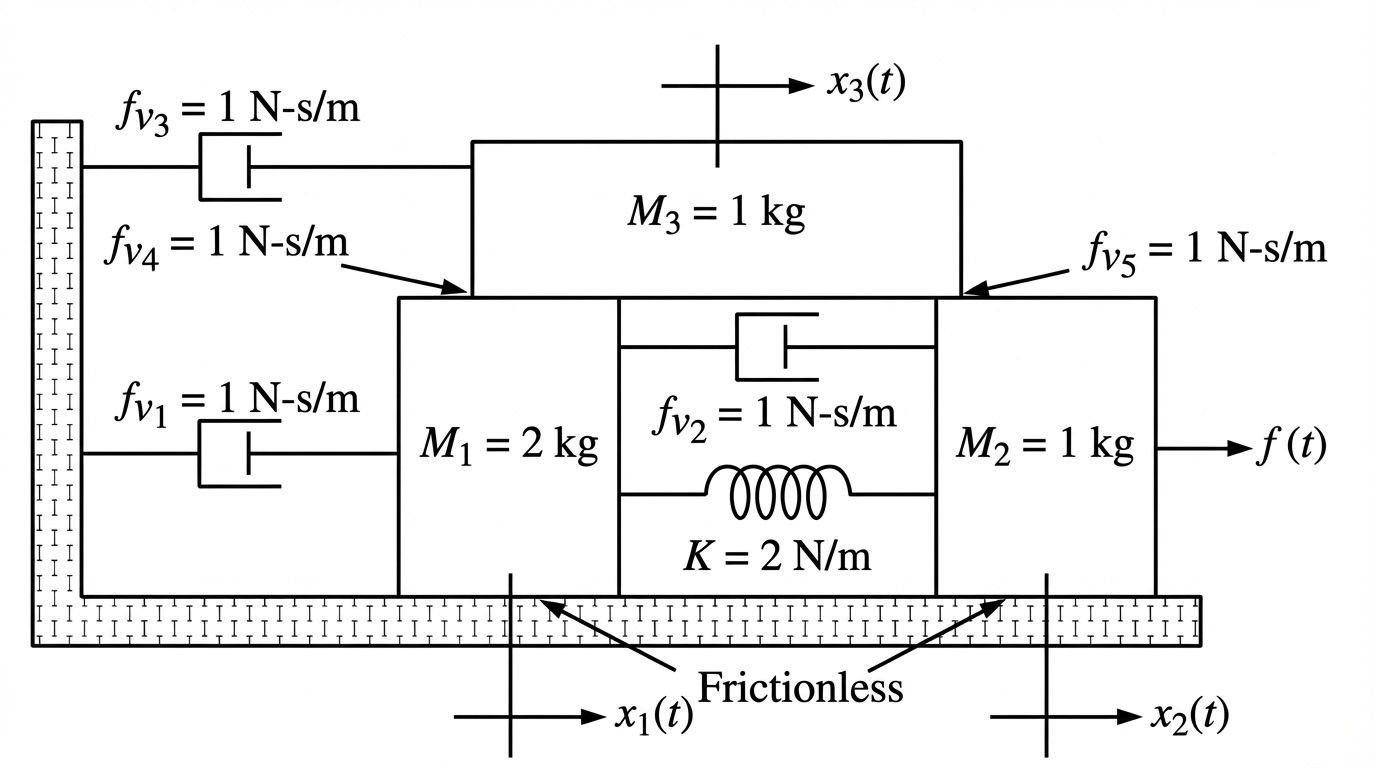
Problem 3

Convert the following transfer functions shown below to state-space representation.

Problem 4

Find the transfer function for each of the SSRs shown below.

a.

$$\dot{\mathbf{x}} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -3 & -2 & -5 \end{bmatrix} \mathbf{x} + \begin{bmatrix} 0 \\ 0 \\ 10 \end{bmatrix} r$$

$$y = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \mathbf{x}$$

b.

$$\dot{\mathbf{x}} = \begin{bmatrix} 2 & -3 & -8 \\ 0 & 5 & 3 \\ -3 & -5 & -4 \end{bmatrix} \mathbf{x} + \begin{bmatrix} 1 \\ 4 \\ 6 \end{bmatrix} r$$

$$y = \begin{bmatrix} 1 & 3 & 6 \end{bmatrix} \mathbf{x}$$

c.

$$\dot{\mathbf{x}} = \begin{bmatrix} 3 & -5 & 2 \\ 1 & -8 & 7 \\ -3 & -6 & 2 \end{bmatrix} \mathbf{x} + \begin{bmatrix} 5 \\ -3 \\ 2 \end{bmatrix} r$$

$$y = \begin{bmatrix} 1 & -4 & 3 \end{bmatrix} \mathbf{x}$$

Problem 5

Assume a system can be represented by the following state variable equations. The variable $d_{0}$ is input to the system. Write the equations in $\dot{\mathbf{x}} = \mathbf{Ax} + \mathbf{Bu}$ format.

$$\frac{dx_0}{dt} = a_{00}x_0 + a_{02}x_2 + d_0$$

$$\frac{dx_1}{dt} = a_{10}x_0 + a_{11}x_1 + a_{12}x_2$$

$$\frac{dx_2}{dt} = a_{20}x_0 + a_{21}x_1 + a_{22}x_2 + a_{23}x_3 + a_{24}x_4$$

$$\frac{dx_3}{dt} = a_{32}x_2 + a_{33}x_3$$

$$\frac{dx_4}{dt} = a_{42}x_2 + a_{44}x_4$$