Lesson 3

1 Learning Objectives

By the end of this lesson students will be able to:

Create transfer functions of translational mechanical systems
Create transfer functions of rotational mechanical systems
Define linearly independent motion, degrees of freedom

2 Writing DEs for Translational Mechanical Systems

Mechanical systems are analogous to electrical systems in that there are three types of components: springs, dashpots, and masses.

When using mesh analysis with circuits, the number of equations equals the number of loop currents. In mechanical systems, the number of equations equals the number of linearly independent motions.

A linearly independent motion is a point in the mechanical system that can move if everything else is held still; this is usually a mass. The number of linearly independent motions is equal to the degrees of freedom of the system.

2.1 Example 1

Given a single mass, spring, damper system, find $G(s) = \frac{X(s)}{F(s)}$ .

Steps for solving translational mechanical problems:

Hold all points of motion still except for current mass.
Sum forces acting on current mass. Write $f_v s$ for dashpot, $K$ for spring, and $Ms^2$ for mass.
Hold current mass still and move all others. Subtract forces acting on mass.
Solve the resulting equations of motion.

2.2 Example 2

Given the system shown below, find $G(s) = \frac{X_2(s)}{F(s)}$ . Use MATLAB to solve.

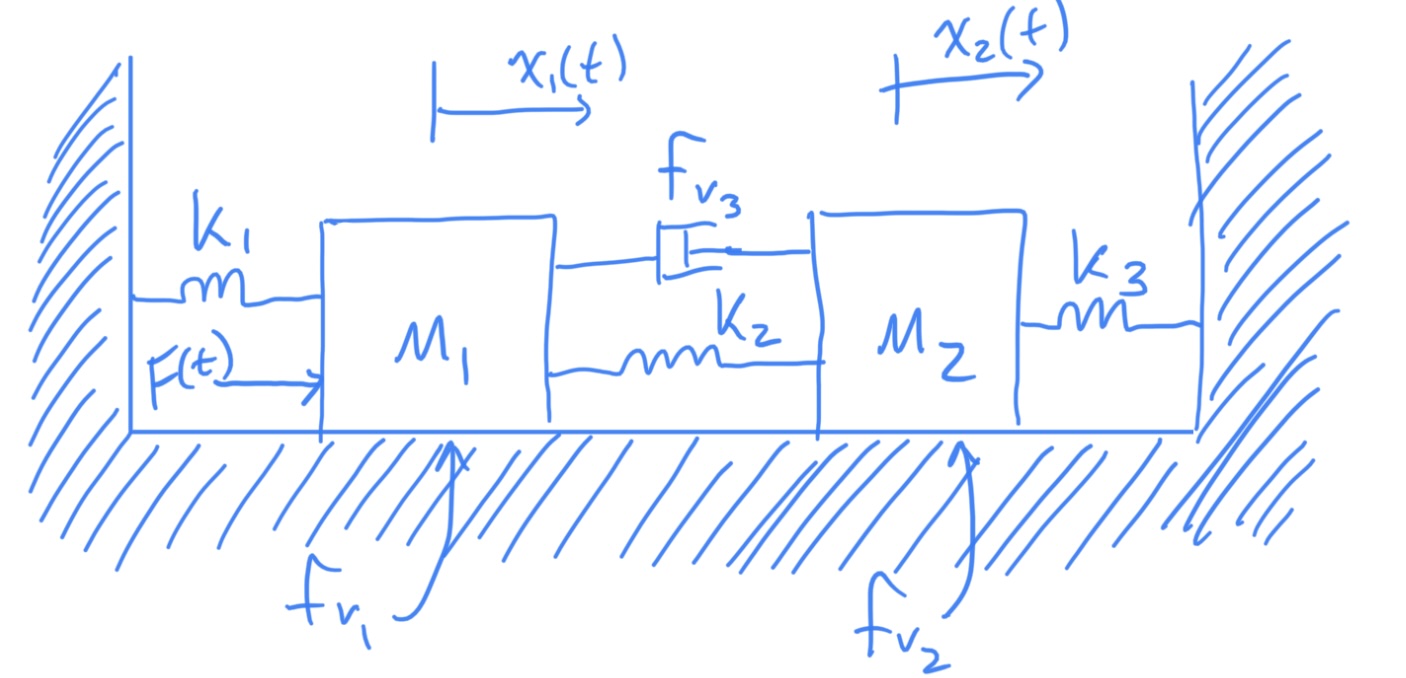
Translational mechanical system for example 2.

syms s x1 x2 x3 f
m1=1; m2=1; fv1=1; fv2=1; fv3=1; k1=1; k2=1; k3=1;
eqn1 = (m1*s^2+(fv1+fv3)*s+(k1+k2))*x1-(fv3*s+k2)*x2 == f;
eqn2 = -(fv3*s+k2)*x1+(m2*s^2+(fv2+fv3)*s+(k2+k3))*x2 == 0;
[x1,x2]=solve([eqn1,eqn2],[x1,x2]);
simplify(x2/f)

2.3 Student Example 1

Given the system shown below, find $G(s) = \frac{X_1(s)}{F(s)}$

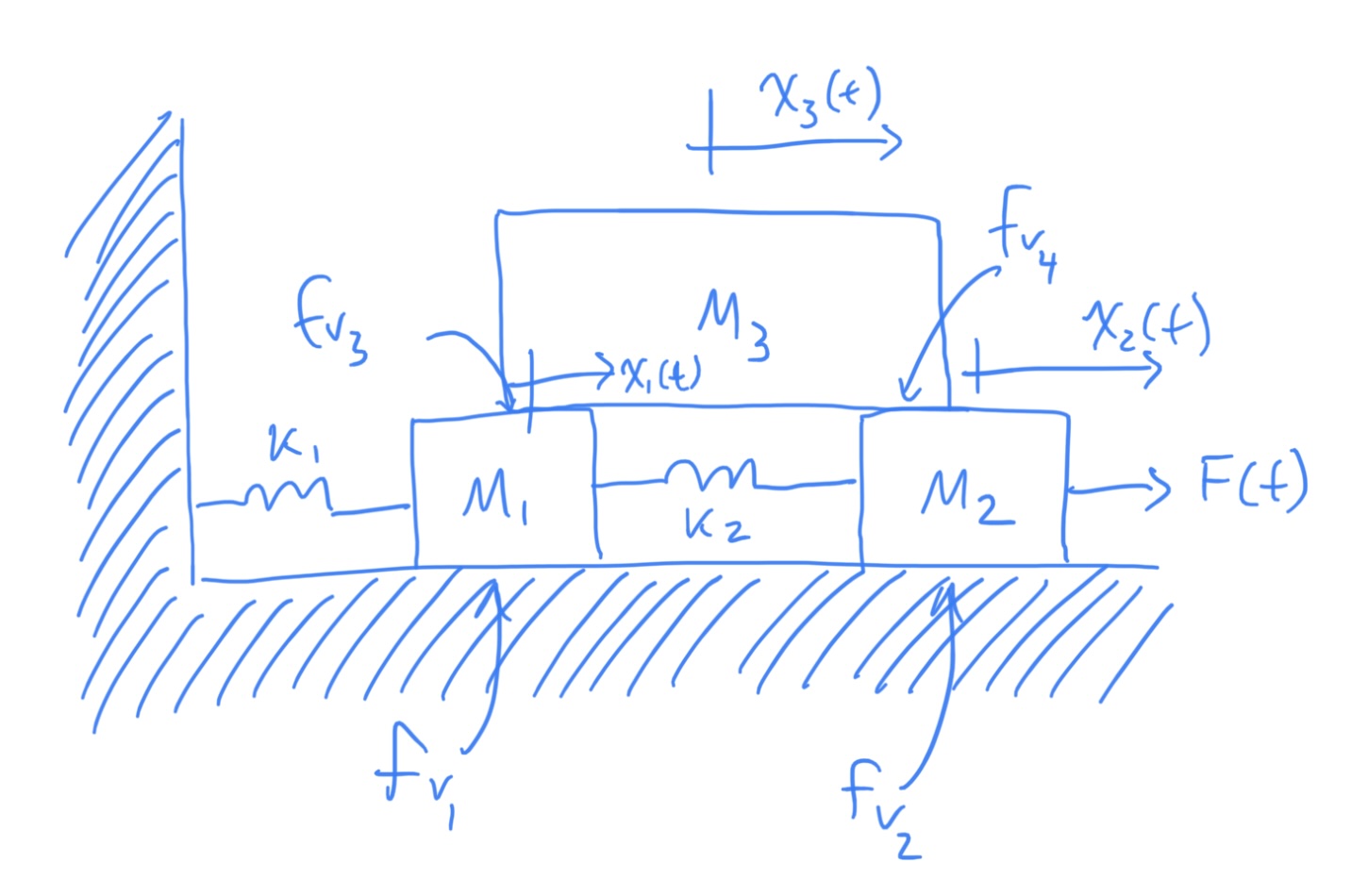
Translational mechanical system for student example 1.

Solution

2.4 Student Example 2

Given the system shown below, find $G(s) = \frac{X_2(s)}{F(s)}$

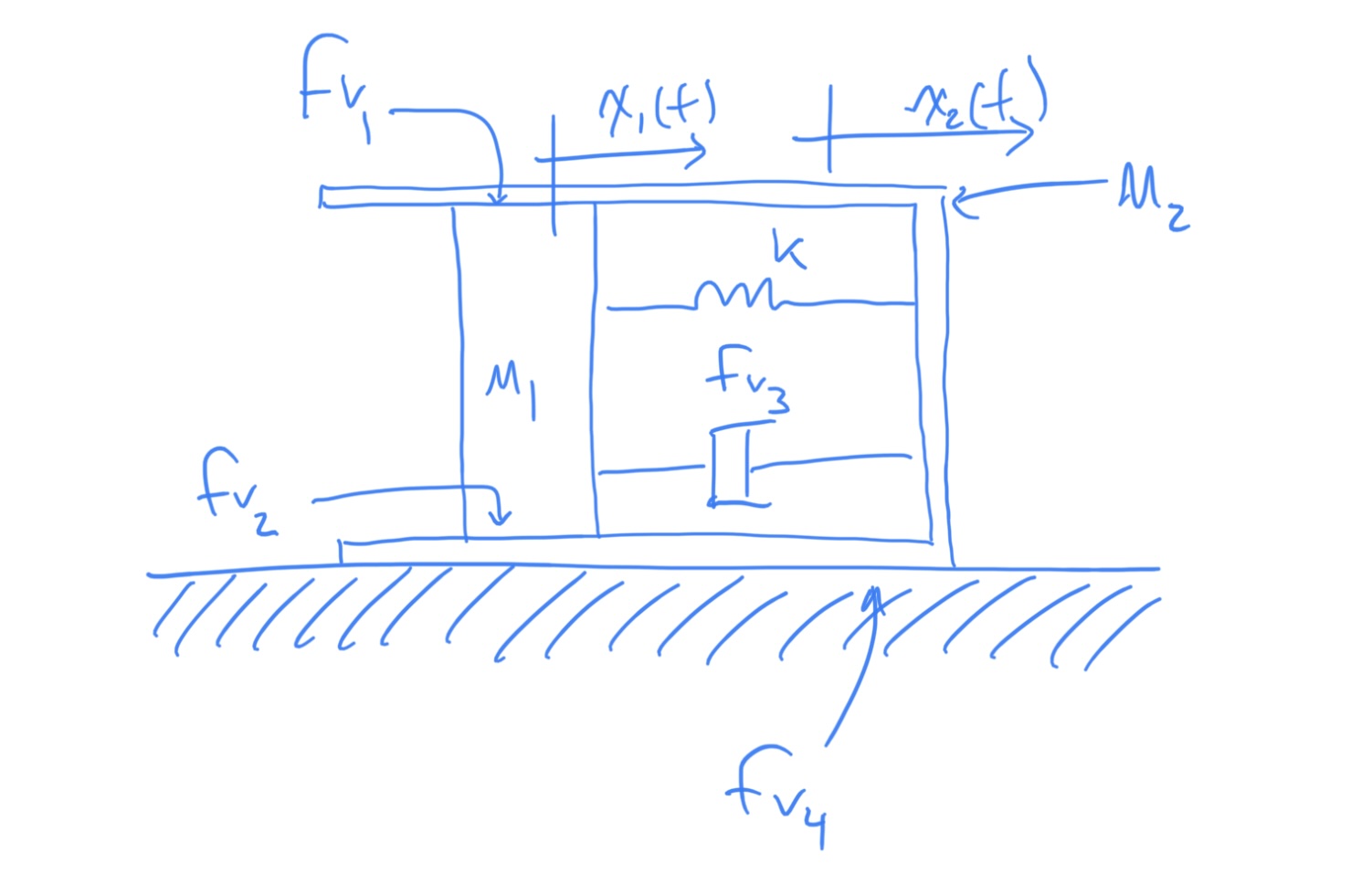
Translational mechanical system for student example 2.

Solution

Sometimes you will see a displacement without a mass.

3 Writing DEs for Rotational Mechanical Systems

Mechanical systems can also be described by rotational parts. A good example is the inner workings of a clock based on gears. The same overall themes that were used with translational systems apply to rotational systems as well.

Use the same steps for rotational systems as we used with translational systems to solve these problems.

3.1 Example 3

Given the system shown below, find $G(s) = \frac{\theta_2(s)}{T(s)}$

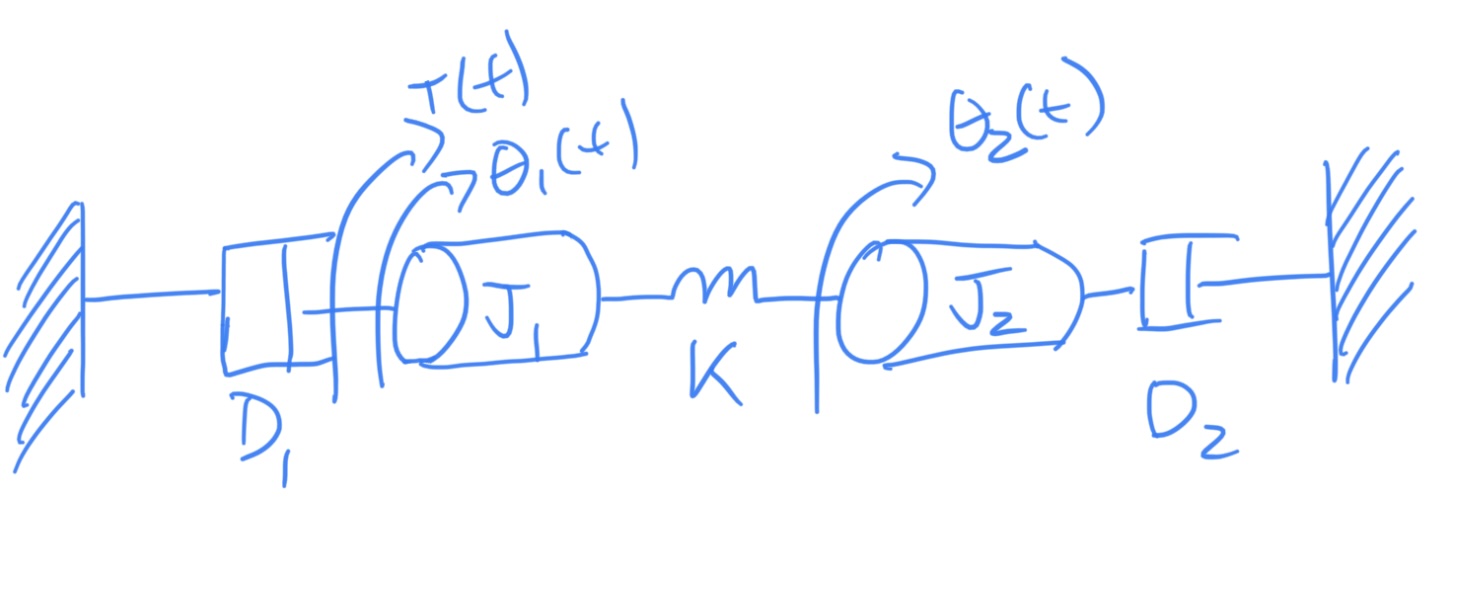
Rotational mechanical system for example 3.

syms s theta1 theta2 t
j1=1; j2=1; d1=1; d2=1; k=1;
eqn1 = (j1*s^2+d1*s+k)*theta1-k*theta2 == t;
eqn2 = -k*theta1+(j2*s^2+d2*s+k)*theta2 == 0;
[theta1,theta2]=solve([eqn1,eqn2],[theta1,theta2]);
simplify(theta2/t)

3.2 Student Example 3

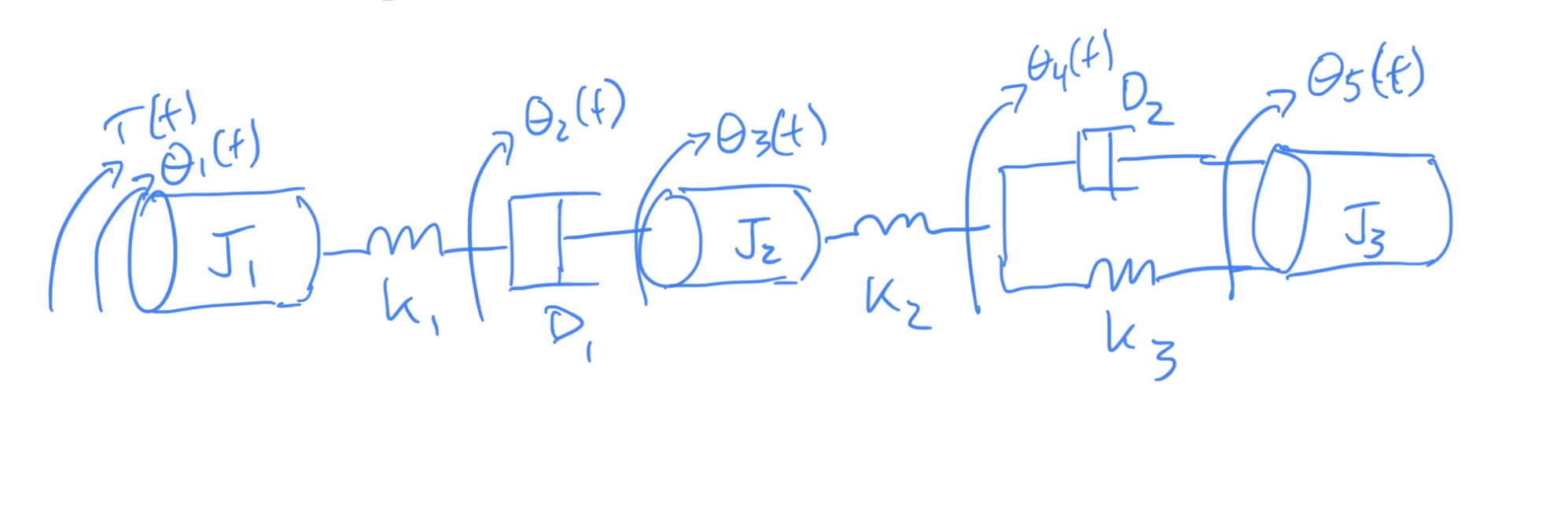
Given the system shown below, find $G(s) = \frac{\theta_2(s)}{T(s)}$

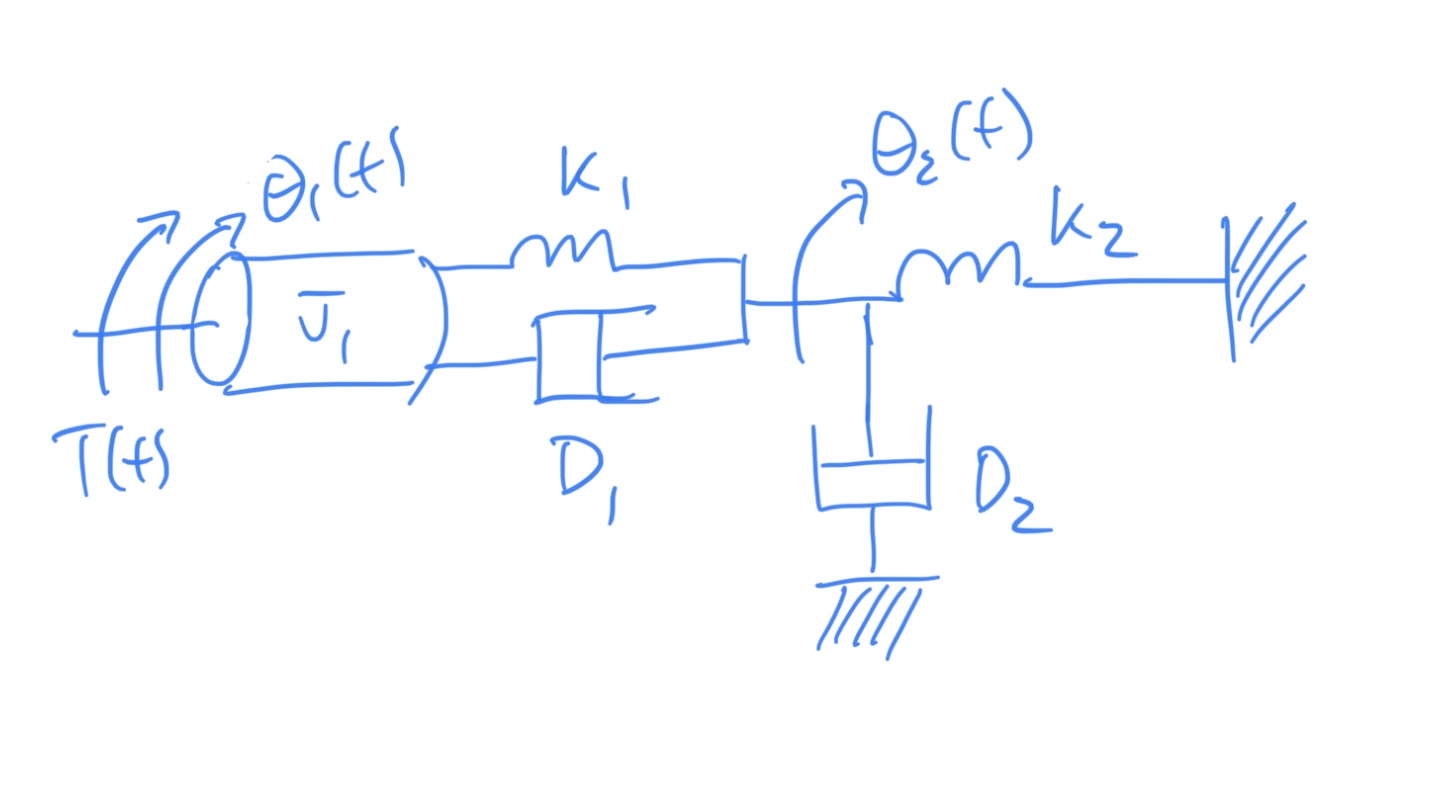
Rotational mechanical system for student example 3.

Solution

3.3 Student Example 4

Given the system shown below, find $G(s) = \frac{\theta_2(s)}{T(s)}$

Rotational mechanical system for student example 4.

Solution