Lesson 6

1 Learning Objectives

By the end of this lesson students will be able to:

• Create a state-space representation of linear, time-invariant systems

2 Introduction

So far we have practiced writing the DEs that describe physical systems. These are often coupled differential equations; the same variables often appear in more than one equation.

We then practiced writing these equations in the form of a transfer function in the LaPlace domain. This method works fine if the system has only one input and one output and is linear. If not, we need another method—state-space.

Summary of the two methods:

1. Classical, or frequency domain
   

• Pro: Easy to see how system will behave (stability and transient response) by looking at equation; easy to adjust settings to desired response
  
• Con: Can only use linear, time-invariant systems (or those that can be approximated as this); initial conditions are always 0

2. Modern, time domain, or state-space
   

• Pro: Can do non-linear systems and systems with nonzero initial conditions; time varying systems too
  
• Con: Not as intuitive

3 State-Variable Equations

All systems have a group of state variables that define all characteristics of a system.

Examples: Current or voltage in circuits, position and velocity in mechanical systems, pressure in fluid systems, concentration in chemical systems.

The state variables are the minimum number of variables that you need to describe the system.

The variable $x_n$ is used to represent the state variables, where $n$ is the total number of state variables; also the order of the system.

The variable $u_r$ is used to represent the input(s), where $r$ is the total number of input variables.

The state-variable equations are $n$ DEs that are the first-order derivatives of each state variable. For example:

$$\dot{x}_{1} = 2x_{1} + 3x_{2} + 4u_{1}$$

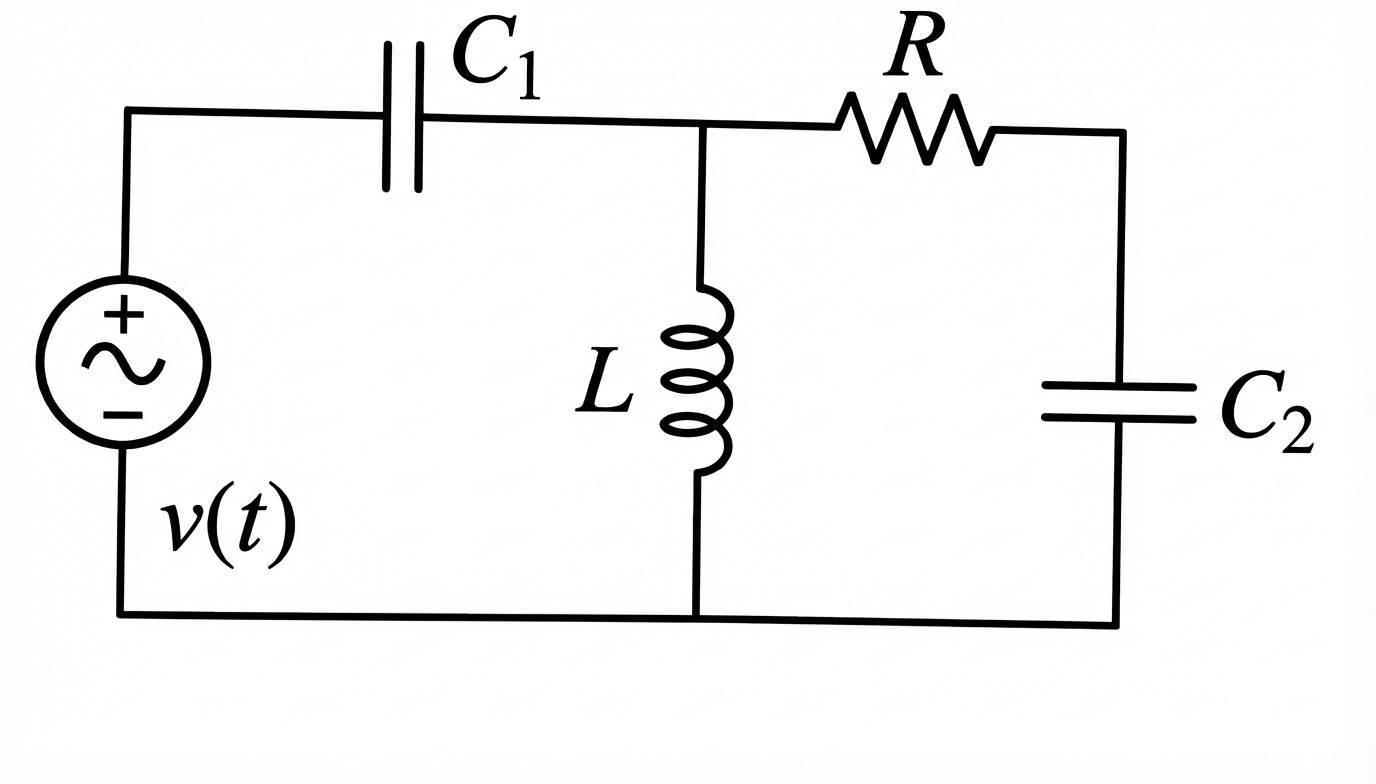
3.1 Example 1

Write the state-variable equations for the system shown below.

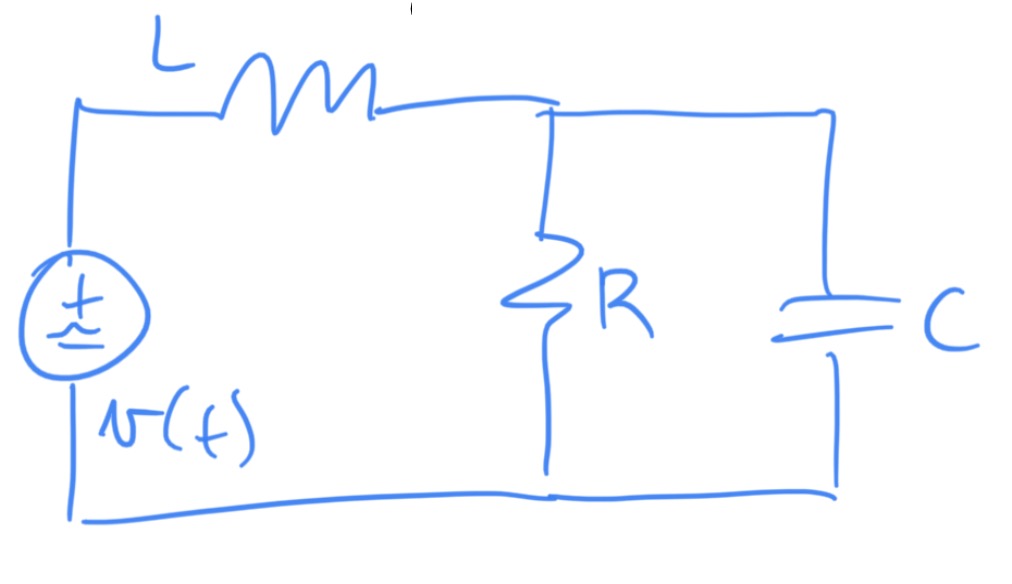
3.2 Student Example 1

Write the state-variable equations for the system shown below.

4 State-Space Representation (SSR)

We just derived state-variable equations for two different systems. If the DEs are linear, we can write them in vector-matrix format:

1. The state-variable equation:

$$\dot{\mathbf{x}} = \mathbf{Ax} + \mathbf{Bu}$$

2. The output equation:

$$\mathbf{y} = \mathbf{Cx} + \mathbf{Du}$$

Each of these letters stand for:

• x = state vector (vector of state variables)
• $\dot{\mathbf{x}}$ = derivative of x
• y = output vector (vector of output equations)
• u = input or control vector
• A = system matrix
• B = input matrix
• C = output matrix
• D = feed-forward matrix

A quick refresher on how matrix multiplication works:

So if we want to convert the following state-variable equations into $\dot{\mathbf{x}} = \mathbf{Ax} + \mathbf{Bu}$ matrix-vector format:

$$\dot{x}_{1} = -6.2x_{1} - 2.3x_{2} + 8.4x_{3}$$ $$\dot{x}_{2} = -x_{2} + 2.7x_{3} + 3u_{1}$$ $$\dot{x}_{3} = -4.1x_{1} - 1.5x_{2} + 3.9x_{3} + 4u_{2}$$

Here’s how we do it:

$$\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{bmatrix} = \begin{bmatrix} -6.2 & -2.3 & 8.4 \\ 0 & -1 & 2.7 \\ -4.1 & -1.5 & 3.9 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 3 & 0 \\ 0 & 4 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}$$

5 State-Space Representation of Electrical Systems

Now, we go back to our previous examples and convert them into correct state-space representation.

5.1 Example 1, cont’d

Write state variable equations in state-space representation. Assume output is $v_{c2}(t)$.

5.2 Student Example 1, cont’d

Write state variable equations in state-space representation. Assume output is current through the resistor, $i_r$.

6 State-Space Representation of Mechanical Systems

Much easier as you just need to write the equations for each mass.

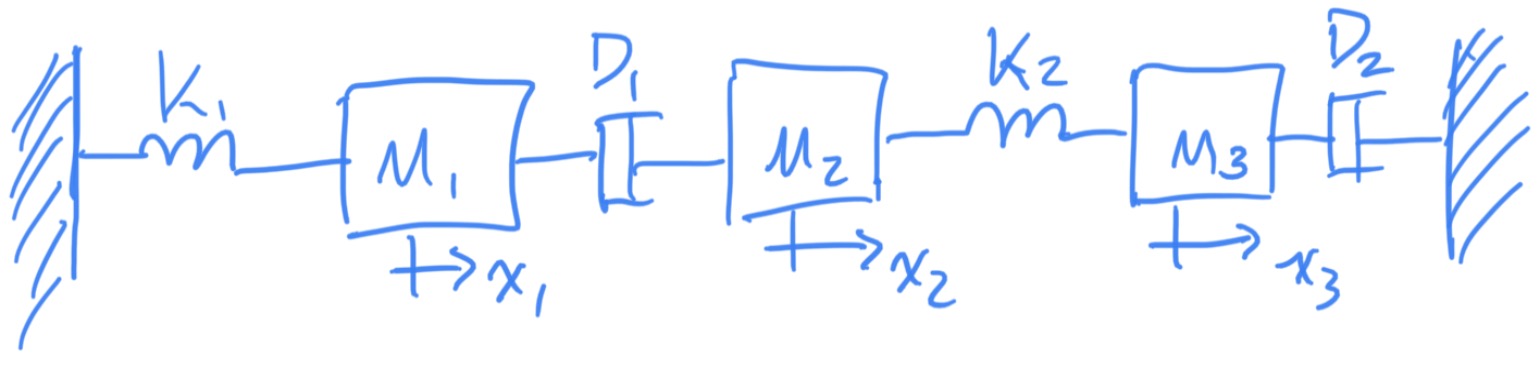
6.1 Example 2

Write the state-space representation of the system below. Assume there is no output.

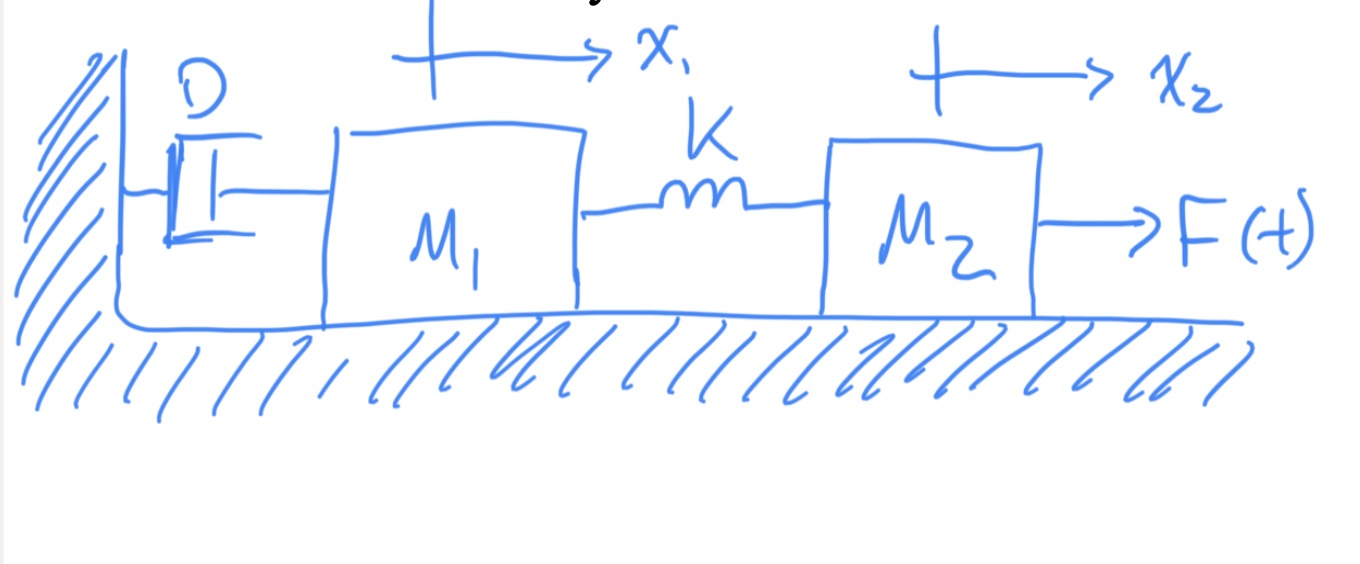
6.2 Student Example 2

Write the state-space representation of the system below. Assume the output is $x_{3}(t)$.